參考
最小二乘法 Least Squares最小二乘法又稱最小平方法,是一種數學方法,透過最小的誤差平方和來找出最佳的參數或一些問題,工程上應該算是系統判別裡一門學問。最常見的應用應該就是在迴歸分析或稱為擬合(regression or fitting)上,下面舉一個例子:
假設有 3 個資料座標,我想找出一條直線 L:y = ax + b 的 a, b 使得這 3 個座標到直線的距離合有最小值,其實就是找出這 3 筆資料的迴歸線,如下圖所示

方法一定義一函數 F
=ax_%7Bi%7D+b-y_%7Bi%7D)
其 F 的平方合表示成 Q,其中 N 為資料數,當有 3 筆資料,N = 3
=%5Csum_%7Bi=1%7D%5E%7BN%7DF_%7Bi%7D(a,%5C,b)%5E%7B2%7D=%5Csum_%7Bi=1%7D%5E%7BN%7D(ax_%7Bi%7D+b-y_%7Bi%7D)%5E%7B2%7D)
欲使 Q 為最小值,必有

依上述條件計算出結果
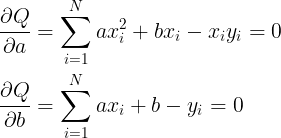
整理成矩陣形式
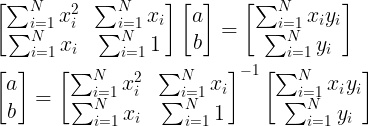
這裡就可以計算出直線 L 的參數了,若是想使用 C 語言或是其他程式來計算的話,建議直接用高斯消去法來處理,因為運算量上面,高斯消去法較低於逆矩陣的運算量。
方法二另一種方法是計算聯立方程式,

將上式表示下列形式

因為 A 矩陣並不是方陣,所以左邊同時乘上自己的轉置,轉換成方陣後就可以求逆矩陣了
%5E%7B-1%7DA%5E%7BT%7DB&space;%5Cend%7Balign*%7D)
展開上式, 可以得到下面的結果
%5E%7B-1%7D&space;%5Cbegin%7Bbmatrix%7D&space;x_%7B1%7D&space;&&space;x_%7B2%7D&space;&&space;x_%7B3%7D%5C%5C&space;1&space;&&space;1&space;&&space;1&space;%5Cend%7Bbmatrix%7D&space;%5Cbegin%7Bbmatrix%7D&space;y_%7B1%7D%5C%5C&space;y_%7B2%7D%5C%5C&space;y_%7B3%7D&space;%5Cend%7Bbmatrix%7D%5C%5C&space;&%5Cbegin%7Bbmatrix%7D&space;a%5C%5C&space;b&space;%5Cend%7Bbmatrix%7D&space;=&space;%5Cbegin%7Bbmatrix%7D&space;%5Csum_%7Bi=1%7D%5E%7BN%7Dx_%7Bi%7D%5E%7B2%7D&space;&&space;%5Csum_%7Bi=1%7D%5E%7BN%7Dx_%7Bi%7D%5C%5C&space;%5Csum_%7Bi=1%7D%5E%7BN%7Dx_%7Bi%7D&space;&&space;%5Csum_%7Bi=1%7D%5E%7BN%7D1&space;%5Cend%7Bbmatrix%7D&space;%5E%7B-1%7D&space;%5Cbegin%7Bbmatrix%7D&space;%5Csum_%7Bi=1%7D%5E%7BN%7Dx_%7Bi%7Dy_%7Bi%7D%5C%5C&space;%5Csum_%7Bi=1%7D%5E%7BN%7Dy_%7Bi%7D&space;%5Cend%7Bbmatrix%7D&space;%5Cend%7Balign*%7D)
結果與方法一是一樣的。
這是一種 LS 的應用,LS 就是一種找出誤差合最小(不一定為 0)的模型參數的方法。
|